C++ for Loop Read Every Other Line

seven. Iteration¶

Computers are often used to automate repetitive tasks. Repeating identical or similar tasks without making errors is something that computers practice well and people exercise poorly.

Repeated execution of a set of statements is called iteration. Because iteration is so common, Python provides several linguistic communication features to make information technology easier. Nosotros've already seen the for statement in chapter 3. This the the form of iteration you'll probable be using almost oft. But in this chapter nosotros've going to look at the while statement — another way to have your plan do iteration, useful in slightly different circumstances.

Before nosotros do that, let'southward simply review a few ideas...

7.1. Assignment¶

As we accept mentioned previously, information technology is legal to make more 1 assignment to the same variable. A new assignment makes an existing variable refer to a new value (and stop referring to the old value).

airtime_remaining = 15 print ( airtime_remaining ) airtime_remaining = 7 print ( airtime_remaining )

The output of this programme is:

because the first time airtime_remaining is printed, its value is xv, and the 2d time, its value is vii.

It is peculiarly of import to distinguish between an assignment statement and a Boolean expression that tests for equality. Because Python uses the equal token ( = ) for assignment, it is tempting to interpret a argument similar a = b every bit a Boolean test. Unlike mathematics, it is not! Remember that the Python token for the equality operator is == .

Note also that an equality exam is symmetric, simply assignment is not. For example, if a == 7 and so 7 == a . But in Python, the statement a = vii is legal and vii = a is non.

In Python, an consignment statement can brand two variables equal, but because further assignments can change either of them, they don't accept to stay that way:

a = v b = a # After executing this line, a and b are now equal a = three # After executing this line, a and b are no longer equal

The third line changes the value of a but does non change the value of b , so they are no longer equal. (In some programming languages, a unlike symbol is used for consignment, such as <- or := , to avoid confusion. Some people also think that variable was an unfortunae give-and-take to choose, and instead we should have chosen them assignables. Python chooses to follow common terminology and token usage, also establish in languages similar C, C++, Coffee, and C#, so nosotros utilise the tokens = for assignment, == for equality, and nosotros talk of variables.

7.2. Updating variables¶

When an consignment statement is executed, the correct-hand side expression (i.e. the expression that comes after the assignment token) is evaluated beginning. This produces a value. Then the assignment is made, so that the variable on the left-hand side now refers to the new value.

One of the most common forms of assignment is an update, where the new value of the variable depends on its sometime value. Deduct 40 cents from my airtime balance, or add ane run to the scoreboard.

Line 2 means get the current value of n, multiply it by iii and add together one, and assign the reply to n, thus making n refer to the value. So afterwards executing the two lines to a higher place, n volition point/refer to the integer 16.

If you try to become the value of a variable that has never been assigned to, you'll get an error:

>>> w = 10 + 1 Traceback (almost contempo call last):   File "<interactive input>", line 1, in NameError: name 'x' is not defined

Earlier you lot can update a variable, you have to initialize it to some starting value, usually with a uncomplicated assignment:

runs_scored = 0 ... runs_scored = runs_scored + 1

Line 3 — updating a variable by adding i to it — is very common. Information technology is called an increment of the variable; subtracting ane is chosen a decrement. Sometimes programmers besides talk about bumping a variable, which means the same equally incrementing information technology by 1.

vii.iii. The for loop revisited¶

Remember that the for loop processes each item in a list. Each item in turn is (re-)assigned to the loop variable, and the body of the loop is executed. We saw this example in an earlier chapter:

for f in [ "Joe" , "Zoe" , "Brad" , "Angelina" , "Zuki" , "Thandi" , "Paris" ]: invitation = "Howdy " + f + ". Please come up to my party on Sabbatum!" print ( invitation )

Running through all the items in a list is called traversing the list, or traversal.

Permit united states write a function now to sum up all the elements in a listing of numbers. Do this by mitt starting time, and endeavor to isolate exactly what steps you lot take. Y'all'll find you demand to go along some "running full" of the sum then far, either on a piece of paper, in your head, or in your calculator. Remembering things from 1 pace to the next is precisely why we have variables in a program: so we'll need some variable to remember the "running total". Information technology should be initialized with a value of zero, and so we need to traverse the items in the list. For each item, we'll want to update the running total by adding the side by side number to it.

ane 2 iii four v 6 seven eight ix 10 11 12 thirteen

def mysum ( xs ): """ Sum all the numbers in the list xs, and return the total. """ running_total = 0 for 10 in xs : running_total = running_total + x return running_total # Add tests similar these to your test suite ... test ( mysum ([ 1 , 2 , three , iv ]) == 10 ) test ( mysum ([ 1.25 , 2.5 , one.75 ]) == 5.5 ) test ( mysum ([ 1 , - 2 , 3 ]) == 2 ) test ( mysum ([ ]) == 0 ) test ( mysum ( range ( xi )) == 55 ) # 11 is not included in the listing.

vii.4. The while statement¶

Hither is a fragment of code that demonstrates the utilise of the while statement:

1 2 3 4 v six 7 8 9 ten 11 12

def sum_to ( due north ): """ Return the sum of one+2+three ... north """ ss = 0 v = one while v <= northward : ss = ss + 5 v = v + one return ss # For your test suite exam ( sum_to ( four ) == 10 ) test ( sum_to ( 1000 ) == 500500 )

You tin can almost read the while statement equally if information technology were English. It means, while v is less than or equal to n , continue executing the torso of the loop. Within the body, each fourth dimension, increment v . When 5 passes n , return your accumulated sum.

More than formally, here is precise flow of execution for a while statement:

• Evaluate the condition at line 5, yielding a value which is either Fake or True .
• If the value is Simulated , leave the while statement and go along execution at the next argument (line 8 in this instance).
• If the value is True , execute each of the statements in the body (lines 6 and seven) and then become back to the while argument at line 5.

The body consists of all of the statements indented below the while keyword.

Detect that if the loop condition is False the first time we get loop, the statements in the torso of the loop are never executed.

The body of the loop should change the value of ane or more variables so that eventually the condition becomes false and the loop terminates. Otherwise the loop will echo forever, which is chosen an infinite loop. An endless source of entertainment for computer scientists is the observation that the directions on shampoo, "soap, rinse, repeat", are an infinite loop.

In the case hither, we tin prove that the loop terminates considering we know that the value of n is finite, and we can see that the value of v increments each time through the loop, so eventually it will have to exceed n . In other cases, it is not then easy, even impossible in some cases, to tell if the loop volition always terminate.

What yous will observe here is that the while loop is more work for you — the developer — than the equivalent for loop. When using a while loop one has to manage the loop variable yourself: give it an initial value, test for completion, then make sure you change something in the body so that the loop terminates. By comparison, here is an equivalent function that uses for instead:

def sum_to ( due north ): """ Return the sum of 1+two+3 ... n """ ss = 0 for v in range ( north + one ): ss = ss + v return ss

Discover the slightly tricky call to the range function — we had to add i onto n , considering range generates its list up to but excluding the value you give it. It would be like shooting fish in a barrel to make a programming mistake and overlook this, but because we've made the investment of writing some unit tests, our test suite would accept defenseless our fault.

Then why have 2 kinds of loop if for looks easier? This next case shows a instance where we need the extra power that we get from the while loop.

seven.v. The Collatz 3n + ane sequence¶

Allow'southward look at a elementary sequence that has fascinated and foxed mathematicians for many years. They still cannot answer even quite uncomplicated questions about this.

The "computational rule" for creating the sequence is to start from some given northward , and to generate the side by side term of the sequence from n , either by halving north , (whenever due north is even), or else by multiplying it by three and adding 1. The sequence terminates when n reaches 1.

This Python function captures that algorithm:

def seq3np1 ( northward ): """ Print the 3n+1 sequence from due north, terminating when it reaches 1. """ while north != 1 : print ( due north , stop = ", " ) if n % 2 == 0 : # n is even north = n // 2 else : # n is odd north = n * 3 + 1 print ( n , terminate = ". \n " )

Detect first that the impress office on line 6 has an extra statement end=", " . This tells the impress part to follow the printed string with whatsoever the developer chooses (in this instance, a comma followed by a space), instead of ending the line. And so each time something is printed in the loop, it is printed on the same output line, with the numbers separated by commas. The call to print(n, end=".\n") at line 11 afterward the loop terminates will then print the terminal value of north followed by a period and a newline character. (You'll cover the \n (newline character) in the next chapter).

The condition for continuing with this loop is northward != 1 , so the loop will continue running until it reaches its termination condition, (i.e. n == 1 ).

Each time through the loop, the program outputs the value of n and and then checks whether information technology is fifty-fifty or odd. If information technology is even, the value of n is divided by 2 using integer division. If information technology is odd, the value is replaced by northward * 3 + 1 . Hither are some examples:

                >>>                                seq3np1                (                3                )                3, ten, v, 16, eight, 4, ii, ane.                >>>                                seq3np1                (                19                )                nineteen, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13,                                  40, 20, 10, 5, 16, 8, 4, 2, i.                >>>                                seq3np1                (                21                )                21, 64, 32, 16, 8, 4, 2, 1.                >>>                                seq3np1                (                16                )                xvi, 8, iv, 2, 1.                >>>              

Since northward sometimes increases and sometimes decreases, there is no obvious proof that n will ever reach 1, or that the programme terminates. For some item values of due north , nosotros can bear witness termination. For case, if the starting value is a power of two, then the value of northward volition be even each fourth dimension through the loop until information technology reaches ane. The previous example ends with such a sequence, starting with 16.

Come across if you tin find a small-scale starting number that needs more a hundred steps before it terminates.

Particular values bated, the interesting question was first posed past a German mathematician chosen Lothar Collatz: the Collatz conjecture (also known every bit the 3n + ane conjecture), is that this sequence terminates for all positive values of n . So far, no ane has been able to prove it or disprove information technology! (A conjecture is a statement that might exist true, but nobody knows for certain.)

Recollect carefully about what would be needed for a proof or disproof of the theorize "All positive integers volition eventually converge to ane using the Collatz rules". With fast computers nosotros have been able to examination every integer upward to very big values, and and so far, they have all eventually ended up at 1. But who knows? Perhaps there is some equally-nevertheless untested number which does not reduce to 1.

Yous'll detect that if you don't stop when you lot reach 1, the sequence gets into its own cyclic loop: 1, iv, ii, ane, 4, 2, 1, 4 ... And then one possibility is that at that place might exist other cycles that we just haven't institute withal.

Wikipedia has an informative commodity well-nigh the Collatz conjecture. The sequence also goes nether other names (Hailstone sequence, Wonderous numbers, etc.), and you'll find out just how many integers have already been tested past calculator, and found to converge!

Choosing between for and while

Use a for loop if you know, before you start looping, the maximum number of times that you'll need to execute the body. For example, if yous're traversing a list of elements, you lot know that the maximum number of loop iterations you can possibly need is "all the elements in the list". Or if you need to impress the 12 times table, we know correct abroad how many times the loop volition demand to run.

So whatsoever problem like "iterate this conditions model for 1000 cycles", or "search this list of words", "find all prime numbers up to 10000" advise that a for loop is best.

By dissimilarity, if y'all are required to echo some computation until some condition is met, and yous cannot summate in advance when (of if) this will happen, equally we did in this 3n + 1 problem, you'll need a while loop.

We call the offset case definite iteration — we know ahead of time some definite premises for what is needed. The latter case is chosen indefinite iteration — nosotros're not sure how many iterations we'll need — we cannot even establish an upper spring!

7.6. Tracing a program¶

To write effective computer programs, and to build a good conceptual model of program execution, a developer needs to develop the ability to trace the execution of a computer plan. Tracing involves becoming the figurer and following the menstruum of execution through a sample programme run, recording the state of all variables and any output the program generates after each didactics is executed.

To understand this process, allow'southward trace the phone call to seq3np1(3) from the previous section. At the outset of the trace, we have a variable, northward (the parameter), with an initial value of 3. Since three is not equal to 1, the while loop body is executed. 3 is printed and iii % 2 == 0 is evaluated. Since it evaluates to False , the else branch is executed and 3 * 3 + 1 is evaluated and assigned to n .

To continue runway of all this every bit you hand trace a program, make a cavalcade heading on a piece of paper for each variable created equally the program runs and some other i for output. Our trace so far would wait something like this:

                n               output printed so far                --              ---------------------                3               3,                10              

Since 10 != 1 evaluates to True , the loop trunk is again executed, and 10 is printed. 10 % 2 == 0 is truthful, so the if co-operative is executed and n becomes v. Past the cease of the trace nosotros have:

                n               output printed so far                --              ---------------------                3               3,                10              iii, 10,                v               3, ten, five,                16              3, 10, 5, xvi,                8               3, ten, 5, sixteen, 8,                iv               3, 10, v, 16, 8, iv,                2               three, 10, 5, 16, eight, four, 2,                1               3, 10, 5, 16, 8, 4, ii, 1.              

Tracing tin can exist a bit dull and error prone (that's why we get computers to do this stuff in the start place!), but it is an essential skill for a programmer to accept. From this trace we tin can learn a lot about the way our code works. We can find that as soon as n becomes a ability of two, for example, the program will require log_two(n) executions of the loop body to complete. We tin also run across that the terminal 1 will non be printed every bit output inside the body of the loop, which is why we put the special print function at the stop.

Tracing a program is, of course, related to single-stepping through your lawmaking and existence able to inspect the variables. Using the estimator to single-footstep for you is less error decumbent and more convenient. Also, equally your programs get more complex, they might execute many millions of steps before they go to the code that yous're really interested in, so manual tracing becomes impossible. Beingness able to fix a breakpoint where you need one is far more than powerful. And so we strongly encourage you to invest time in learning using to use your programming surroundings (PyScripter, in these notes) to full consequence.

In that location are likewise some great visualization tools becoming available to help yous trace and empathise small fragments of Python code. The one we recommend is at http://netserv.ict.ru.ac.za/python3_viz

We've cautioned confronting chatterbox functions, but used them here. Equally we learn a chip more Python, we'll be able to show you how to generate a listing of values to hold the sequence, rather than having the function impress them. Doing this would remove the need to have all these pesky impress functions in the eye of our logic, and will make the function more useful.

vii.7. Counting digits¶

The following function counts the number of decimal digits in a positive integer:

def num_digits ( northward ): count = 0 while n != 0 : count = count + 1 n = north // 10 render count

A call to print(num_digits(710)) will impress 3 . Trace the execution of this function phone call (perhaps using the unmarried step role in PyScripter, or the Python visualizer, or on some newspaper) to convince yourself that it works.

This function demonstrates an of import design of computation chosen a counter. The variable count is initialized to 0 and and so incremented each fourth dimension the loop body is executed. When the loop exits, count contains the result — the full number of times the loop body was executed, which is the aforementioned every bit the number of digits.

If nosotros wanted to only count digits that are either 0 or five, adding a conditional earlier incrementing the counter will do the play tricks:

def num_zero_and_five_digits ( n ): count = 0 while due north > 0 : digit = northward % 10 if digit == 0 or digit == 5 : count = count + 1 due north = n // 10 return count

Confirm that exam(num_zero_and_five_digits(1055030250) == 7) passes.

Notice, however, that test(num_digits(0) == 1) fails. Explain why. Do y'all recollect this is a bug in the code, or a bug in the specifications, or our expectations, or the tests?

7.eight. Abbreviated assignment¶

Incrementing a variable is and so common that Python provides an abbreviated syntax for it:

                >>>                                count                =                0                >>>                                count                +=                one                >>>                                count                ane                >>>                                count                +=                1                >>>                                count                two              

count += 1 is an abreviation for count = count + 1 . We pronounce the operator as "plus-equals". The increment value does not have to be i:

                >>>                                n                =                2                >>>                                n                +=                5                >>>                                n                seven              

In that location are similar abbreviations for -= , *= , /= , //= and %= :

                >>>                                northward                =                two                >>>                                n                *=                5                >>>                                n                ten                >>>                                n                -=                4                >>>                                n                half-dozen                >>>                                northward                //=                2                >>>                                n                3                >>>                                n                %=                2                >>>                                n                1              

7.10. Tables¶

One of the things loops are good for is generating tables. Before computers were readily available, people had to calculate logarithms, sines and cosines, and other mathematical functions by mitt. To make that easier, mathematics books independent long tables listing the values of these functions. Creating the tables was slow and boring, and they tended to be full of errors.

When computers appeared on the scene, one of the initial reactions was, "This is great! Nosotros tin utilize the computers to generate the tables, so there volition be no errors." That turned out to exist true (mostly) but shortsighted. Shortly thereafter, computers and calculators were so pervasive that the tables became obsolete.

Well, almost. For some operations, computers use tables of values to get an approximate reply and then perform computations to ameliorate the approximation. In some cases, there have been errors in the underlying tables, nigh famously in the table the Intel Pentium processor chip used to perform floating-point division.

Although a log table is not as useful equally information technology once was, it notwithstanding makes a good example of iteration. The following program outputs a sequence of values in the left column and 2 raised to the power of that value in the correct column:

for x in range ( xiii ): # Generate numbers 0 to 12 print ( x , " \t " , ii ** ten )

The string "\t" represents a tab character. The backslash character in "\t" indicates the beginning of an escape sequence. Escape sequences are used to represent invisible characters similar tabs and newlines. The sequence \n represents a newline.

An escape sequence tin appear anywhere in a string; in this example, the tab escape sequence is the only matter in the cord. How do yous recall you represent a backslash in a string?

As characters and strings are displayed on the screen, an invisible marker called the cursor keeps rails of where the next character will go. After a print office, the cursor unremarkably goes to the get-go of the next line.

The tab character shifts the cursor to the correct until information technology reaches one of the tab stops. Tabs are useful for making columns of text line up, as in the output of the previous plan:

                0       1                1       2                two       4                3       viii                4       16                five       32                6       64                7       128                8       256                9       512                x      1024                xi      2048                12      4096              

Considering of the tab characters between the columns, the position of the 2nd column does non depend on the number of digits in the first column.

7.11. Two-dimensional tables¶

A two-dimensional tabular array is a table where you read the value at the intersection of a row and a column. A multiplication table is a skilful instance. Let's say you want to impress a multiplication tabular array for the values from 1 to 6.

A good way to beginning is to write a loop that prints the multiples of 2, all on one line:

for i in range ( ane , vii ): impress ( two * i , terminate = " " ) print ()

Here we've used the range function, but fabricated it showtime its sequence at 1. As the loop executes, the value of i changes from i to 6. When all the elements of the range have been assigned to i , the loop terminates. Each fourth dimension through the loop, it displays the value of 2 * i , followed by iii spaces.

Over again, the extra terminate=" " argument in the print office suppresses the newline, and uses three spaces instead. Afterward the loop completes, the telephone call to print at line three finishes the current line, and starts a new line.

The output of the programme is:

And then far, then expert. The next step is to encapsulate and generalize.

seven.12. Encapsulation and generalization¶

Encapsulation is the procedure of wrapping a slice of code in a office, allowing y'all to take advantage of all the things functions are practiced for. Yous have already seen some examples of encapsulation, including is_divisible in a previous chapter.

Generalization means taking something specific, such every bit press the multiples of two, and making it more than general, such as press the multiples of any integer.

This part encapsulates the previous loop and generalizes it to impress multiples of northward :

def print_multiples ( due north ): for i in range ( 1 , 7 ): print ( n * i , finish = " " ) print ()

To encapsulate, all nosotros had to do was add together the offset line, which declares the proper name of the role and the parameter listing. To generalize, all we had to practise was replace the value 2 with the parameter north .

If we call this part with the argument 2, nosotros get the same output as before. With the statement 3, the output is:

With the argument 4, the output is:

By now you can probably estimate how to print a multiplication table — by calling print_multiples repeatedly with different arguments. In fact, we can use another loop:

for i in range ( i , seven ): print_multiples ( i )

Observe how like this loop is to the i inside print_multiples . All we did was supercede the print function with a role telephone call.

The output of this plan is a multiplication table:

                1      2      3      iv      5      six                2      four      6      viii      x     12                3      6      9      12     15     eighteen                4      8      12     16     20     24                5      10     15     xx     25     thirty                vi      12     xviii     24     30     36              

vii.13. More than encapsulation¶

To demonstrate encapsulation again, let's take the code from the last section and wrap it up in a function:

def print_mult_table (): for i in range ( 1 , 7 ): print_multiples ( i )

This procedure is a mutual evolution plan. Nosotros develop lawmaking by writing lines of lawmaking outside whatever function, or typing them in to the interpreter. When nosotros become the code working, nosotros extract it and wrap it up in a function.

This evolution program is particularly useful if you don't know how to divide the program into functions when you outset writing. This approach lets yous design equally you go along.

vii.14. Local variables¶

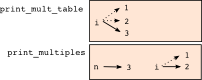
Y'all might be wondering how we can apply the same variable, i , in both print_multiples and print_mult_table . Doesn't information technology crusade problems when one of the functions changes the value of the variable?

The answer is no, because the i in print_multiples and the i in print_mult_table are not the same variable.

Variables created inside a role definition are local; you tin't access a local variable from outside its home function. That means y'all are complimentary to have multiple variables with the same name as long as they are not in the same function.

Python examines all the statements in a office — if any of them assign a value to a variable, that is the clue that Python uses to make the variable a local variable.

The stack diagram for this program shows that the two variables named i are not the same variable. They can refer to different values, and changing one does non touch on the other.

The value of i in print_mult_table goes from ane to half dozen. In the diagram it happens to exist iii. The next time through the loop it will exist 4. Each time through the loop, print_mult_table calls print_multiples with the current value of i every bit an argument. That value gets assigned to the parameter northward .

Within print_multiples , the value of i goes from 1 to vi. In the diagram, information technology happens to be ii. Changing this variable has no event on the value of i in print_mult_table .

It is mutual and perfectly legal to have dissimilar local variables with the same proper noun. In particular, names like i and j are used often as loop variables. If you avoid using them in i function but because yous used them somewhere else, you lot will probably make the program harder to read.

The visualizer at http://netserv.ict.ru.ac.za/python3_viz/ shows very clearly how the two variables i are singled-out variables, and how they take independent values.

7.15. The break statement¶

The break statement is used to immediately leave the body of its loop. The next statement to exist executed is the first one after the trunk:

for i in [ 12 , 16 , 17 , 24 , 29 ]: if i % 2 == 1 : # If the number is odd break # ... immediately go out the loop print ( i ) print ( "done" )

This prints:

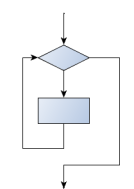
The pre-test loop — standard loop behaviour

for and while loops do their tests at the outset, before executing whatever role of the body. They're called pre-exam loops, because the test happens before (pre) the body. break and render are our tools for adapting this standard behaviour.

7.16. Other flavours of loops¶

Sometimes we'd like to have the middle-test loop with the get out test in the middle of the body, rather than at the kickoff or at the cease. Or a post-test loop that puts its go out test as the concluding thing in the torso. Other languages have unlike syntax and keywords for these dissimilar flavours, merely Python just uses a combination of while and if condition: intermission to get the job done.

A typical example is a problem where the user has to input numbers to exist summed. To indicate that there are no more than inputs, the user enters a special value, frequently the value -ane, or the empty string. This needs a middle-exit loop blueprint: input the next number, then examination whether to exit, or else procedure the number:

The middle-test loop flowchart

full = 0 while True : response = input ( "Enter the adjacent number. (Get out blank to finish)" ) if response == "" : break total += int ( response ) impress ( "The total of the numbers you entered is " , total )

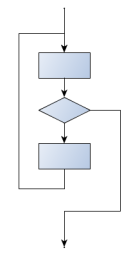
Convince yourself that this fits the middle-exit loop flowchart: line three does some useful piece of work, lines 4 and v can exit the loop, and if they don't line 6 does more useful work earlier the adjacent iteration starts.

The while bool-expr: uses the Boolean expression to determine whether to iterate again. True is a trivial Boolean expression, so while True: means always do the loop body over again. This is a language idiom — a convention that most programmers will recognize immediately. Since the expression on line 2 volition never finish the loop, (information technology is a dummy test) the programmer must arrange to break (or return) out of the loop body elsewhere, in some other mode (i.e. in lines 4 and 5 in this sample). A clever compiler or interpreter will understand that line 2 is a fake exam that must ever succeed, and so it won't even generate a exam, and our flowchart never even put the diamond-shape dummy test box at the peak of the loop!

Similarly, by just moving the if condition: break to the stop of the loop body we create a pattern for a post-examination loop. Post-test loops are used when you desire to exist sure that the loop body always executes at least once (because the offset exam simply happens at the end of the execution of the first loop body). This is useful, for example, if nosotros want to play an interactive game confronting the user — we always want to play at least one game:

while True : play_the_game_once () response = input ( "Play again? (yeah or no)" ) if response != "yep" : break print ( "Goodbye!" )

Hint: Think about where you want the exit exam to happen

In one case you lot've recognized that you need a loop to repeat something, call back about its terminating condition — when will I want to end iterating? Then figure out whether you need to do the exam before starting the showtime (and every other) iteration, or at the end of the first (and every other) iteration, or perhaps in the middle of each iteration. Interactive programs that require input from the user or read from files often need to leave their loops in the heart or at the terminate of an iteration, when it becomes articulate that in that location is no more information to procedure, or the user doesn't desire to play our game anymore.

7.17. An example¶

The following program implements a elementary guessing game:

1 2 3 iv 5 half dozen seven 8 ix 10 11 12 13 14 15 16 17 eighteen

import random # Nosotros cover random numbers in the rng = random . Random () # modules chapter, so peek ahead. number = rng . randrange ( 1 , 1000 ) # Become random number between [1 and 1000). guesses = 0 msg = "" while True : guess = int ( input ( msg + " \due north Judge my number between 1 and 1000: " )) guesses += 1 if judge > number : msg += str ( guess ) + " is too loftier. \n " elif gauge < number : msg += str ( guess ) + " is too depression. \n " else : intermission input ( " \n\n Bang-up, you got information technology in {0} guesses! \due north\n " . format ( guesses ))

This programme makes utilize of the mathematical constabulary of trichotomy (given real numbers a and b, exactly one of these 3 must be true: a > b, a < b, or a == b).

At line 18 there is a phone call to the input function, but we don't practise anything with the issue, non even assign it to a variable. This is legal in Python. Here it has the outcome of popping up the input dialog window and waiting for the user to respond before the programme terminates. Programmers ofttimes use the fox of doing some extra input at the end of a script, only to keep the window open.

Also find the utilize of the msg variable, initially an empty string, on lines half dozen, 12 and 14. Each time through the loop we extend the message being displayed: this allows us to display the program's feedback right at the same place equally we're asking for the adjacent guess.

7.xviii. The continue statement¶

This is a control catamenia argument that causes the plan to immediately skip the processing of the residuum of the body of the loop, for the current iteration. But the loop still carries on running for its remaining iterations:

for i in [ 12 , 16 , 17 , 24 , 29 , 30 ]: if i % 2 == 1 : # If the number is odd continue # Don't process it print ( i ) print ( "done" )

This prints:

7.19. More generalization¶

Every bit another instance of generalization, imagine you wanted a program that would impress a multiplication tabular array of any size, not simply the vi-by-six table. You could add a parameter to print_mult_table :

def print_mult_table ( loftier ): for i in range ( 1 , high + 1 ): print_multiples ( i )

Nosotros replaced the value seven with the expression loftier+1 . If we call print_mult_table with the statement 7, information technology displays:

                one      2      iii      iv      5      6                2      4      6      8      10     12                iii      half dozen      9      12     15     18                4      8      12     xvi     xx     24                five      10     15     xx     25     30                half-dozen      12     18     24     30     36                vii      fourteen     21     28     35     42              

This is fine, except that nosotros probably want the table to be square — with the aforementioned number of rows and columns. To do that, we add some other parameter to print_multiples to specify how many columns the table should accept.

Merely to exist annoying, we call this parameter high , demonstrating that different functions can take parameters with the same name (just like local variables). Here'south the whole program:

def print_multiples ( n , high ): for i in range ( 1 , loftier + 1 ): impress ( n * i , end = " " ) print () def print_mult_table ( high ): for i in range ( 1 , high + 1 ): print_multiples ( i , high )

Discover that when we added a new parameter, we had to change the first line of the function (the function heading), and nosotros as well had to change the place where the part is chosen in print_mult_table .

Now, when we call print_mult_table(7) :

                ane      two      3      4      5      6      7                2      iv      half dozen      8      10     12     14                3      6      ix      12     15     18     21                four      8      12     xvi     20     24     28                5      ten     15     20     25     30     35                6      12     18     24     30     36     42                seven      14     21     28     35     42     49              

When you generalize a function appropriately, you often get a program with capabilities you didn't plan. For example, you might observe that, because ab = ba, all the entries in the table appear twice. You could save ink by press only half the table. To exercise that, you just have to modify one line of print_mult_table . Change

print_multiples ( i , high + ane )

to

and y'all become:

ane two      iv 3      6      ix four      8      12     xvi 5      ten     xv     20     25 6      12     18     24     30     36 7      14     21     28     35     42     49

7.20. Functions¶

A few times at present, we have mentioned all the things functions are skilful for. By now, you might exist wondering what exactly those things are. Here are some of them:

1. Capturing your mental chunking. Breaking your complex tasks into sub-tasks, and giving the sub-tasks a meaningful proper noun is a powerful mental technique. Await back at the example that illustrated the post-test loop: nosotros assumed that we had a office chosen play_the_game_once . This chunking allowed united states of america to put aside the details of the detail game — is it a bill of fare game, or noughts and crosses, or a function playing game — and simply focus on one isolated part of our plan logic — letting the histrion choose whether they desire to play once more.
2. Dividing a long plan into functions allows yous to separate parts of the program, debug them in isolation, and and so etch them into a whole.
3. Functions facilitate the use of iteration.
4. Well-designed functions are often useful for many programs. Once you write and debug 1, y'all can reuse it.

7.21. Paired Data¶

We've already seen lists of names and lists of numbers in Python. We're going to peek ahead in the textbook a little, and show a more advanced way of representing our data. Making a pair of things in Python is as uncomplicated as putting them into parentheses, like this:

year_born = ( "Paris Hilton" , 1981 )

Nosotros can put many pairs into a list of pairs:

celebs = [( "Brad Pitt" , 1963 ), ( "Jack Nicholson" , 1937 ), ( "Justin Bieber" , 1994 )]

Hither is a quick sample of things nosotros tin do with structured data similar this. Starting time, print all the celebs:

print ( celebs ) print ( len ( celebs ))

                  [("Brad Pitt", 1963), ("Jack Nicholson", 1937), ("Justin Bieber", 1994)]                  3                

Notice that the celebs list has just iii elements, each of them pairs.

Now we print the names of those celebrities built-in before 1980:

for ( nm , yr ) in celebs : if yr < 1980 : print ( nm )

This demonstrates something we accept not seen yet in the for loop: instead of using a unmarried loop control variable, we've used a pair of variable names, (nm, yr) , instead. The loop is executed three times — once for each pair in the listing, and on each iteration both the variables are assigned values from the pair of data that is being handled.

seven.22. Nested Loops for Nested Data¶

Now nosotros'll come upwards with an fifty-fifty more audacious listing of structured data. In this case, we take a list of students. Each student has a name which is paired up with some other listing of subjects that they are enrolled for:

students = [ ( "John" , [ "CompSci" , "Physics" ]), ( "Vusi" , [ "Maths" , "CompSci" , "Stats" ]), ( "Jess" , [ "CompSci" , "Accounting" , "Economics" , "Management" ]), ( "Sarah" , [ "InfSys" , "Accounting" , "Economics" , "CommLaw" ]), ( "Zuki" , [ "Sociology" , "Economics" , "Law" , "Stats" , "Music" ])]

Here we've assigned a list of five elements to the variable students . Let's impress out each student proper noun, and the number of subjects they are enrolled for:

# Impress all students with a count of their courses. for ( proper noun , subjects ) in students : print ( proper name , "takes" , len ( subjects ), "courses" )

Python agreeably responds with the following output:

                John takes two courses                Vusi takes iii courses                Jess takes 4 courses                Sarah takes 4 courses                Zuki takes 5 courses              

Now nosotros'd like to ask how many students are taking CompSci. This needs a counter, and for each educatee we need a second loop that tests each of the subjects in turn:

# Count how many students are taking CompSci counter = 0 for ( name , subjects ) in students : for s in subjects : # A nested loop! if south == "CompSci" : counter += 1 print ( "The number of students taking CompSci is" , counter )

                  The number of students taking CompSci is 3                

You should set a list of your own data that interests y'all — perhaps a listing of your CDs, each containing a list of song titles on the CD, or a listing of movie titles, each with a list of movie stars who acted in the moving picture. You could then ask questions like "Which movies starred Angelina Jolie?"

7.23. Newton's method for finding square roots¶

Loops are often used in programs that compute numerical results by starting with an approximate reply and iteratively improving it.

For example, earlier we had calculators or computers, people needed to calculate foursquare roots manually. Newton used a particularly proficient method (there is some evidence that this method was known many years earlier). Suppose that yous want to know the square root of n . If you start with near whatsoever approximation, yous tin compute a better approximation (closer to the bodily answer) with the following formula:

better = ( approx + n / approx ) / 2

Repeat this calculation a few times using your estimator. Can y'all run across why each iteration brings your guess a little closer? I of the amazing properties of this particular algorithm is how quickly it converges to an accurate answer — a corking reward for doing it manually.

Past using a loop and repeating this formula until the meliorate approximation gets close enough to the previous one, we tin can write a function for computing the square root. (In fact, this is how your calculator finds square roots — information technology may take a slightly different formula and method, but information technology is as well based on repeatedly improving its guesses.)

This is an case of an indefinite iteration problem: nosotros cannot predict in accelerate how many times we'll want to improve our guess — we just want to keep getting closer and closer. Our stopping condition for the loop will be when our old guess and our improved approximate are "close enough" to each other.

Ideally, we'd like the old and new judge to exist exactly equal to each other when we stop. But exact equality is a tricky notion in reckoner arithmetics when real numbers are involved. Because existent numbers are not represented absolutely accurately (later all, a number similar pi or the square root of two has an infinite number of decimal places considering it is irrational), nosotros need to formulate the stopping test for the loop past asking "is a close enough to b"? This stopping condition can exist coded like this:

if abs ( a - b ) < 0.001 : # Make this smaller for better accuracy break

Notice that we accept the absolute value of the difference between a and b !

This trouble is also a expert example of when a middle-get out loop is appropriate:

1 2 3 4 v 6 seven 8 nine 10 xi 12

def sqrt ( northward ): approx = n / 2.0 # Start with some or other guess at the answer while True : meliorate = ( approx + n / approx ) / 2.0 if abs ( approx - meliorate ) < 0.001 : return better approx = improve # Test cases impress ( sqrt ( 25.0 )) print ( sqrt ( 49.0 )) print ( sqrt ( 81.0 ))

The output is:

Meet if you can ameliorate the approximations past changing the stopping status. Besides, step through the algorithm (peradventure past hand, using your calculator) to run into how many iterations were needed before information technology achieved this level of accuracy for sqrt(25) .

7.24. Algorithms¶

Newton's method is an example of an algorithm: it is a mechanical process for solving a category of bug (in this instance, computing square roots).

Some kinds of cognition are not algorithmic. For example, learning dates from history or your multiplication tables involves memorization of specific solutions.

Merely the techniques you learned for improver with carrying, subtraction with borrowing, and long division are all algorithms. Or if yous are an avid Sudoku puzzle solver, you might accept some specific ready of steps that you always follow.

I of the characteristics of algorithms is that they do not require any intelligence to carry out. They are mechanical processes in which each step follows from the last according to a simple set of rules. And they're designed to solve a general class or category of problems, not just a single problem.

Understanding that hard issues tin can exist solved by step-by-stride algorithmic processes (and having engineering science to execute these algorithms for us) is one of the major breakthroughs that has had enormous benefits. So while the execution of the algorithm may exist wearisome and may crave no intelligence, algorithmic or computational thinking — i.e. using algorithms and automation as the basis for approaching problems — is chop-chop transforming our social club. Some claim that this shift towards algorithmic thinking and processes is going to have even more impact on our society than the invention of the printing press. And the process of designing algorithms is interesting, intellectually challenging, and a primal part of what nosotros call programming.

Some of the things that people do naturally, without difficulty or conscious thought, are the hardest to express algorithmically. Understanding tongue is a good example. We all do it, but and then far no one has been able to explicate how we practice information technology, at least non in the form of a stride-by-step mechanical algorithm.

7.25. Glossary¶

algorithm

A step-by-step process for solving a category of problems.

body

The statements within a loop.

breakpoint

A place in your plan lawmaking where program execution will pause (or break), assuasive you to audit the country of the program'southward variables, or single-pace through individual statements, executing them 1 at a fourth dimension.

bump

Programmer slang. Synonym for increase.

continue statement

A statement that causes the remainder of the current iteration of a loop to exist skipped. The flow of execution goes back to the top of the loop, evaluates the condition, and if this is true the adjacent iteration of the loop will begin.

counter

A variable used to count something, usually initialized to null and incremented in the body of a loop.

cursor

An invisible marker that keeps track of where the side by side grapheme will be printed.

decrement

Decrease by 1.

definite iteration

A loop where we have an upper bound on the number of times the body will exist executed. Definite iteration is commonly best coded as a for loop.

development programme

A process for developing a program. In this affiliate, we demonstrated a mode of development based on developing code to exercise simple, specific things and then encapsulating and generalizing.

encapsulate

To divide a large complex plan into components (similar functions) and isolate the components from each other (by using local variables, for example).

escape sequence

An escape character, \, followed by one or more printable characters used to designate a nonprintable grapheme.

generalize

To replace something unnecessarily specific (like a constant value) with something appropriately full general (like a variable or parameter). Generalization makes lawmaking more versatile, more likely to be reused, and sometimes even easier to write.

increase

Both equally a noun and as a verb, increment means to increment by ane.

space loop

A loop in which the terminating status is never satisfied.

indefinite iteration

A loop where nosotros just need to keep going until some status is met. A while statement is used for this case.

initialization (of a variable)

To initialize a variable is to give it an initial value. Since in Python variables don't exist until they are assigned values, they are initialized when they are created. In other programming languages this is not the example, and variables can be created without being initialized, in which case they have either default or garbage values.

iteration

Repeated execution of a gear up of programming statements.

loop

The construct that allows allows united states to repeatedly execute a statement or a grouping of statements until a terminating condition is satisfied.

loop variable

A variable used every bit role of the terminating condition of a loop.

meta-notation

Extra symbols or notation that helps draw other notation. Here we introduced square brackets, ellipses, italics, and bold as meta-notation to help depict optional, repeatable, substitutable and fixed parts of the Python syntax.

middle-test loop

A loop that executes some of the body, and then tests for the exit condition, and then may execute some more of the body. Nosotros don't have a special Python construct for this case, only tin use while and break together.

nested loop

A loop within the trunk of another loop.

newline

A special character that causes the cursor to motion to the beginning of the next line.

post-test loop

A loop that executes the body, and then tests for the leave status. We don't have a special Python construct for this, simply can use while and interruption together.

pre-test loop

A loop that tests before deciding whether the execute its body. for and while are both pre-test loops.

unmarried-step

A mode of interpreter execution where you are able to execute your programme one step at a fourth dimension, and inspect the consequences of that step. Useful for debugging and building your internal mental model of what is going on.

tab

A special character that causes the cursor to move to the side by side tab stop on the current line.

trichotomy

Given any real numbers a and b, exactly 1 of the following relations holds: a < b, a > b, or a == b. Thus when you tin found that 2 of the relations are false, you tin assume the remaining 1 is true.

trace

To follow the flow of execution of a program by hand, recording the change of state of the variables and any output produced.

7.26. Exercises¶

This chapter showed united states how to sum a list of items, and how to count items. The counting example also had an if statement that let the states only count some selected items. In the previous chapter nosotros also showed a function find_first_2_letter_word that allowed us an "early go out" from inside a loop by using return when some condition occurred. We now as well have break to exit a loop (but not the enclosing function, and go along to carelessness the current iteration of the loop without ending the loop.

Limerick of list traversal, summing, counting, testing conditions and early on leave is a rich collection of building blocks that can be combined in powerful ways to create many functions that are all slightly unlike.

The first six questions are typical functions y'all should be able to write using only these building blocks.

1. Write a office to count how many odd numbers are in a list.

2. Sum up all the even numbers in a list.

3. Sum up all the negative numbers in a list.

4. Count how many words in a list have length 5.

5. Sum all the elements in a listing up to merely non including the starting time even number. (Write your unit tests. What if at that place is no even number?)

6. Count how many words occur in a listing upwards to and including the first occurrence of the word "sam". (Write your unit tests for this example too. What if "sam" does not occur?)

7. Add a print part to Newton'south sqrt office that prints out better each time it is calculated. Call your modified role with 25 every bit an argument and record the results.

8. Trace the execution of the last version of print_mult_table and figure out how information technology works.

9. Write a function print_triangular_numbers(n) that prints out the start n triangular numbers. A call to print_triangular_numbers(5) would produce the post-obit output:

   (hint: employ a spider web search to find out what a triangular number is.)

10. Write a function, is_prime , which takes a single integer statement and returns True when the argument is a prime number number and False otherwise. Add tests for cases like this:

                      test                  (                  is_prime                  (                  11                  ))                  test                  (                  not                  is_prime                  (                  35                  ))                  exam                  (                  is_prime                  (                  19911121                  ))                

    The last case could represent your birth date. Were you born on a prime twenty-four hour period? In a class of 100 students, how many practise you think would accept prime number birth dates?

11. Revisit the boozer pirate trouble from the exercises in chapter 3. This time, the drunk pirate makes a plough, and and then takes some steps forrard, and repeats this. Our social scientific discipline educatee at present records pairs of data: the angle of each turn, and the number of steps taken later on the turn. Her experimental data is [(160, twenty), (-43, x), (270, 8), (-43, 12)]. Use a turtle to describe the path taken by our drunk friend.

12. Many interesting shapes can be drawn past the turtle by giving a list of pairs like we did above, where the first item of the pair is the angle to turn, and the second particular is the altitude to move forward. Fix a listing of pairs and so that the turtle draws a house with a cantankerous through the centre, as prove hither. This should exist done without going over whatever of the lines / edges more than once, and without lifting your pen.

    

13. Not all shapes like the one above can be fatigued without lifting your pen, or going over an edge more than once. Which of these tin can exist drawn?

    

    Now read Wikipedia's article(http://en.wikipedia.org/wiki/Eulerian_path) about Eulerian paths. Learn how to tell immediately past inspection whether it is possible to discover a solution or not. If the path is possible, yous'll also know where to put your pen to start drawing, and where you should stop up!

14. What will num_digits(0) return? Modify it to render 1 for this case. Why does a call to num_digits(-24) result in an space loop? (hint: -1//x evaluates to -1) Alter num_digits so that information technology works correctly with any integer value. Add these tests:

                      test                  (                  num_digits                  (                  0                  )                  ==                  1                  )                  test                  (                  num_digits                  (                  -                  12345                  )                  ==                  v                  )                

15. Write a function num_even_digits(n) that counts the number of even digits in n . These tests should pass:

                      test                  (                  num_even_digits                  (                  123456                  )                  ==                  3                  )                  test                  (                  num_even_digits                  (                  2468                  )                  ==                  4                  )                  test                  (                  num_even_digits                  (                  1357                  )                  ==                  0                  )                  test                  (                  num_even_digits                  (                  0                  )                  ==                  1                  )                

16. Write a role sum_of_squares(xs) that computes the sum of the squares of the numbers in the listing xs . For example, sum_of_squares([2, 3, 4]) should return 4+9+16 which is 29:

                      exam                  (                  sum_of_squares                  ([                  ii                  ,                  three                  ,                  4                  ])                  ==                  29                  )                  test                  (                  sum_of_squares                  ([                  ])                  ==                  0                  )                  test                  (                  sum_of_squares                  ([                  2                  ,                  -                  3                  ,                  4                  ])                  ==                  29                  )                

17. You and your friend are in a squad to write a two-player game, human confronting figurer, such as Tic-Tac-Toe / Noughts and Crosses. Your friend volition write the logic to play ane round of the game, while you will write the logic to allow many rounds of play, go along score, decide who plays, first, etc. The two of you negotiate on how the 2 parts of the plan will fit together, and you come with this simple scaffolding (which your friend will amend later):

    1 2 three 4 5 half-dozen 7 8 9 x 11 12 13 xiv 15 16 17

    # Your friend will complete this function def play_once ( human_plays_first ): """ Must play one round of the game. If the parameter is True, the human gets to play start, else the computer gets to play starting time. When the round ends, the return value of the function is one of -1 (human wins), 0 (game drawn), ane (computer wins). """ # This is all dummy scaffolding code right at the moment... import random # See Modules chapter ... rng = random . Random () # Pick a random result between -ane and 1. outcome = rng . randrange ( - 1 , 2 ) impress ( "Human plays kickoff={0}, winner={ane} " . format ( human_plays_first , event )) return result

    1. Write the main program which repeatedly calls this function to play the game, and after each round it announces the issue equally "I win!", "You lot win!", or "Game drawn!". It and then asks the role player "Practise you want to play again?" and either plays again, or says "Goodbye", and terminates.
    2. Keep score of how many wins each player has had, and how many draws in that location have been. After each round of play, too announce the scores.
    3. Add logic so that the players take turns to play first.
    4. Compute the percentage of wins for the human, out of all games played. Also announce this at the stop of each round.
    5. Depict a flowchart of your logic.

quirkbetheareast36.blogspot.com

Source: https://openbookproject.net/thinkcs/python/english3e/iteration.html

Share this post